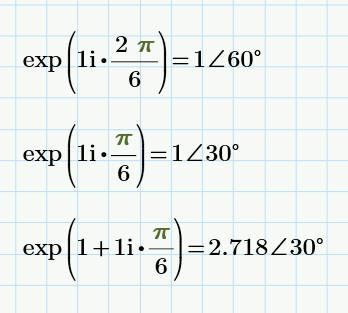мнимая единица
формула Эйлера
извлечение корня
корни полинома
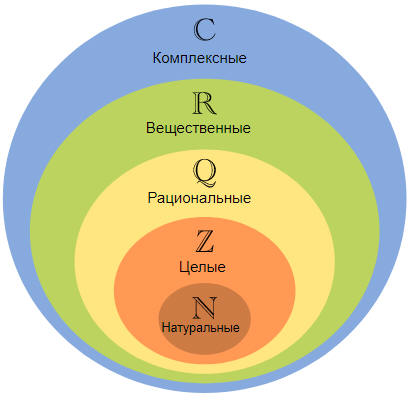
Комплексные числа
Комплексные числа
— числа вида a + b∙i, где i —
мнимая единица, то есть число, для которого выполняется
равенство: i2 = -1. Действия над комплексными числами
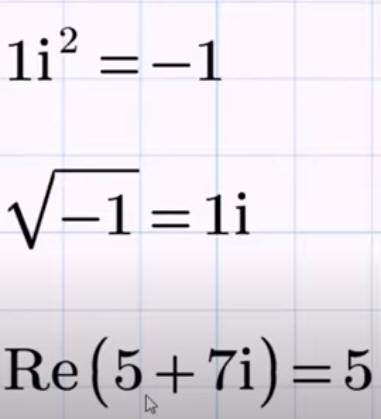
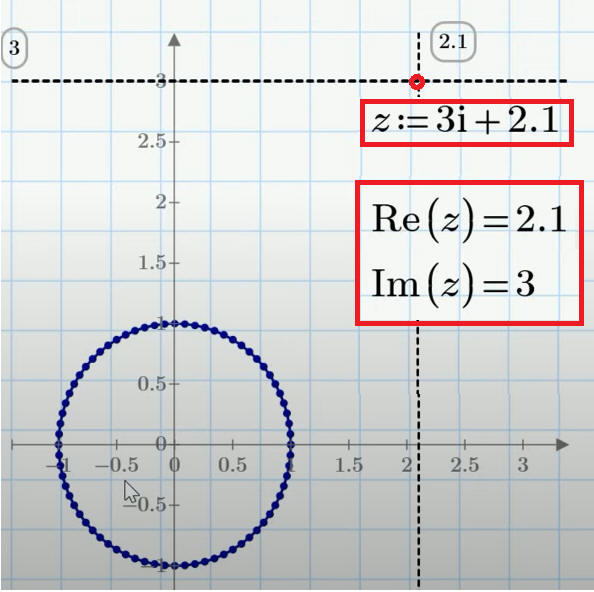
Геометрическая интерпретация комплексных чисел: удобно представлять комплексные числа z = (a,b) = a + b∙i точками на комплексной плоскости.
Например, для изображения
комплексно сопряжённых чисел a + b∙i и a - b∙i используется операция отражения относительно горизонтальной оси.
смотреть на YouTube
Модулем (абсолютной величиной) комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости (или, что то же самое, расстояние от точки комплексной плоскости до начала координат).
Модуль комплексного числа z=x+i∙y обозначается |z|.
Аргументом ненулевого комплексного числа φ называется угол между радиус-вектором соответствующей точки и положительной вещественной полуосью.
Аргумент числа z измеряется в радианах и обозначается Arg(z).
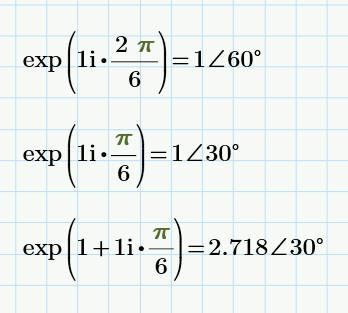
Формула Эйлера
Тригонометрическая форма комплексного числа: z=|z|∙(cosφ + i∙sinφ).
Фундаментальное значение в комплексном анализе имеет
формула Эйлера:
ei∙φ = cosφ + i∙sinφ,
где e — число Эйлера, или основание натурального логарифма, иррациональное и трансцендентное число, приблизительно равное 2,71828.
Комплексная экспонента ei∙φ = exp(i∙φ) продолжает вещественную на случай общего комплексного показателя степени.
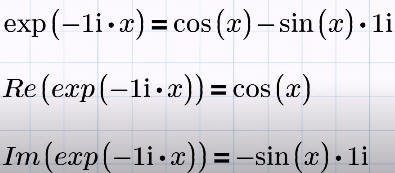
Применяя формулу Эйлера к тригонометрической форме, получим показательную форму комплексного числа:
z=|z|∙ei∙φ.